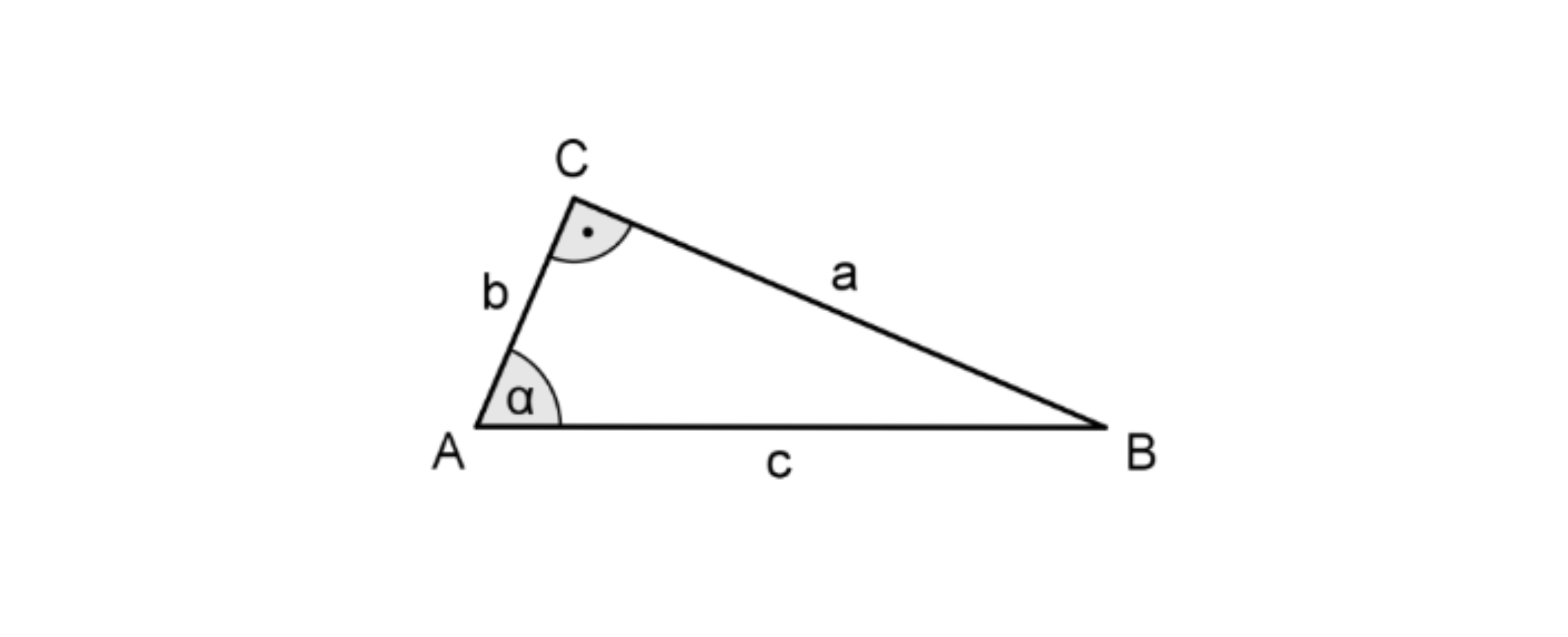
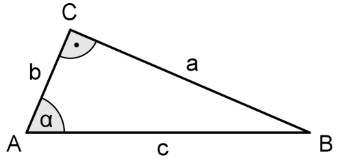
Betrachtet werden rechtwinklige Dreiecke mit rechtem Winkel bei und den in nebenstehender Abbildung verwendeten Bezeichnungen.
a) Berechnen Sie die Seitenlänge , falls gilt: und .
b) Drücken Sie allgemein, also unabhängig von den in Teilaufgabe a) betrachteten Zahlenwerten, und durch die Seitenlängen , und aus und zeigen Sie mithilfe dieser Ausdrücke, dass in jedem rechtwinkligen Dreieck gilt: .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?